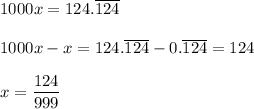Question

Recurring decimal rational of 0,124​

Answer 1

124/999

Explanation:

A recurring decimal fraction can be expressed as a rational number by using the recurring digits in the numerator and an equal number of 9s in the denominator:

`0.\overline{124}=(124)/(999)`

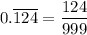
This fraction cannot be reduced.

_____

Additional comment

If the recurring digits don't start at the decimal point, then you can determine the fraction by ...

• Multiply the number by 10^n, where n is the number of recurring digits
• Subtract the original number. This will cancel the recurring part of the number so the difference is a finite decimal.
• Divide by (10^n -1) and simplify the fraction.

In this case, you would get ...

`1000x = 124.\overline{124}\\\\1000x-x=124.\overline{124}-0.\overline{124}=124\\\\x=(124)/(999)`