Answer:
(15.9,16.1) is the required 98% confidence interval for mean usage of electricity.
Explanation:
We are given the following in the question:
Sample mean,
 = 16 kWh
= 16 kWh
Sample size, n = 3394
Alpha, α = 0.02
Population standard deviation, σ = 2.5 kWh
98% Confidence interval:
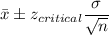
Putting the values, we get,
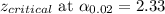
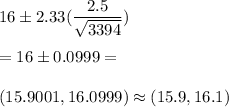
(15.9,16.1) is the required 98% confidence interval for mean usage of electricity.