Question

A survey was conducted regarding the new policy on lunch time in a certain corporate. Forty-six out of one hundred people who participated in this survey support the new policy. Estimate the standard error of the estimated proportion of employees in the corporate supporting the new policy (round off to second decimal place).

Answer 1

Standard error = 0.05

Explanation:

We are given the following in the question:

Sample size, n = 100

Number of people who support the new policy, x = 46

Sample proportion:

`\hat{p} = (x)/(n) = (46)/(100) = 0.46`

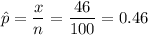
Formula for standard error of estimated proportion:

`S.E = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

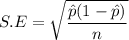
Putting values, we get,

`S.E = \sqrt{(0.46(1-0.46))/(100)} = 0.0498\approx 0.05`

Thus, the 0.05 is the standard error of the estimated proportion of employees in the corporate supporting the new policy.