The correct option is iv. On a coordinate plane, a cubic root function approaches x = negative 4 in quadrant 3, has a point of inflection at (negative 2, negative 5), and then decreases and approaches the negative y-axis in quadrant 3.
To determine the graph of
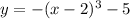 , we can analyze its characteristics. The negative sign outside the parentheses reflects the graph vertically, making it open downward. The cube function inside indicates a cubic shape.
, we can analyze its characteristics. The negative sign outside the parentheses reflects the graph vertically, making it open downward. The cube function inside indicates a cubic shape.
Among the options:
i. Incorrect. It describes a cubic root function approaching the negative y-axis in quadrant 4, but the given function is a cubic function.
ii. Incorrect. This option refers to a cubic root function approaching x = -5 in quadrant 3, not consistent with the given cubic function.
iii. Incorrect. This describes a cubic root function approaching the y-axis in quadrant 4, inconsistent with the downward-opening cubic function.
iv. Correct. This accurately depicts a cubic root function approaching x = -4 in quadrant 3, having a point of inflection at (-2, -5), and decreasing while approaching the negative y-axis in quadrant 3.
Therefore, the correct option is iv, describing the graph of
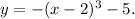
The question probable maybe:
Which of the following is the graph of y = negative (x minus 2) cubed minus 5?
i. On a coordinate plane, a cubic root function approaches the negative y-axis in quadrant 4, has a point of inflection at (2, negative 5), and then increases and approaches x = 4.
ii. On a coordinate plane, a cubic root function approaches x = negative 5 in quadrant 3, has a point of inflection at (negative 2, negative 5), and then approaches the y-axis in quadrant 3.
iii. On a coordinate plane, a cubic root function approaches the y-axis in quadrant 4, has a point of inflection at (2, negative 5), and then decreases and approaches x = 4.
iv. On a coordinate plane, a cubic root function approaches x = negative 4 in quadrant 3, has a point of inflection at (negative 2, negative 5), and then decreases and approaches the negative y-axis in quadrant 3.