Answer:
The hose pipe can fill the pond in 21.465 hours.
The inlet pipe can fill the pond in 20.465 hours.
Explanation:
Given that, a inlet pipe and a hose pipe together can fill the pond in 10 hours.
The inlet pipe alone can fill the pond in one hour less time than the hose pipe can fill the pond.
Let the hose pipe can complete the job in x hours.
Then the inlet pipe can fill the pond in (x-1) hours.
The rate of filling of hose pipe is
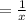
The rate of filling of inlet pipe is
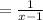
The rate of filling of both pipes is =
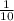
According to the problem,
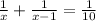
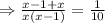 [ simplifying the fraction]
[ simplifying the fraction]
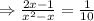
 [ Multiplying 10(x²-x) both sides]
[ Multiplying 10(x²-x) both sides]

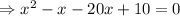 [ simplifying ]
[ simplifying ]
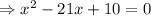
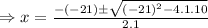 [ applying quadratic formula]
[ applying quadratic formula]
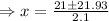
⇒ x= 21.465, -0.465
x= - 0.465 does not possible, since time can not be negative.
∴x=21.465
The hose pipe can fill the pond in 21.465 hours.
The inlet pipe can fill the pond in (21.465-1)=20.465 hours.