Question

The sanitation department of a large city wants to investigate ways to reduce the amount of recyclable materials that are placed in the landfill. They randomly sample 30 households and find that the sample mean amount of waste per household is 9.5 pounds/week and the standard deviation is 11.5 pounds/week. The distribution of the data is slightly right skewed but contains no extreme outliers. Construct a 99% confidence interval for the mean amount of waste per household.

Answer 1

99%, confidence interval for the mean amount of waste per household is [3.713 pounds/week , 15.286 pounds/week].

Explanation:

We are given that the sanitation department of a large city wants to investigate ways to reduce the amount of recyclable materials that are placed in the landfill.

They randomly sample 30 households and find that the sample mean amount of waste per household is 9.5 pounds/week and the standard deviation is 11.5 pounds/week.

Assuming data follows normal distribution.

Firstly, the pivotal quantity for 99% confidence interval for the population mean is given by;

P.Q. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean amount of waste per household = 9.5 pounds/week

n = sample of households = 30

s = sample standard deviation = 11.5 pounds/week

`\mu` = true mean amount of waste per household

Here for constructing 99% confidence interval we have used One-sample t statistics because we don't know about the population standard deviation.

So, 99% confidence interval for the population mean,
`\mu` is ;

P(-2.756 <
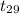`t_2_9` < 2.756) = 0.99 {As the critical value of t at 29 degree

of freedom are -2.756 & 2.756 with P = 0.5%}

P(-2.756 <
`(\bar X-\mu)/((s)/(√(n) ) )` < 2.756) = 0.99

P(
`-2.756 * {(s)/(√(n) ) }` <
`{\bar X-\mu}` <
`2.756 * {(s)/(√(n) ) }` ) = 0.99

P(
`\bar X-2.756 * {(s)/(√(n) ) }` <
`\mu` <
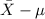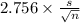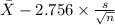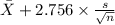`\bar X+2.756 * {(s)/(√(n) ) }` ) = 0.99

99% confidence interval for
`\mu` = [
`\bar X-2.756 * {(s)/(√(n) ) }` ,
`\bar X+2.756 * {(s)/(√(n) ) }`]

= [
`9.5-2.756 * {(11.5)/(√(30) ) }` ,
`9.5+2.756 * {(11.5)/(√(30) ) }` ]

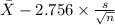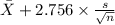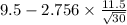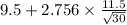= [3.713 pounds/week , 15.286 pounds/week]

Therefore, 99% confidence interval for the mean amount of waste per household is [3.713 pounds/week , 15.286 pounds/week].