Answer: D. 0.57
Step-by-step explanation:
The formula to calculate the eccentricity
 of an ellipse is (assuming the moon's orbit in the shape of an ellipse):
of an ellipse is (assuming the moon's orbit in the shape of an ellipse):
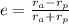
Where:
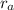 is the apoapsis (the longest distance between the moon and its planet)
is the apoapsis (the longest distance between the moon and its planet)
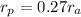 is the periapsis (the shortest distance between the moon and its planet)
is the periapsis (the shortest distance between the moon and its planet)
Then:
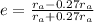
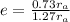
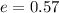 This is the moon's orbital eccentricity
This is the moon's orbital eccentricity