Question

Gabriel wants to build a rectangular pen for his animals. One side of the pen will be against the barn; the other three sides will be enclosed with wire fencing. If Gabriel has 650 feet of fencing

A) What dimensions would maximize the area of the pen?
B) Let w be the width of the enclosure (perpendicular to the barn) and let l be the length of the enclosure (parallel to the barn). Write an function for the area A of the enclosure in terms of w.
C) What width w would maximize the area?
D) What is the maximum area?

Answer 1

(a) 162.5 ft by 325 ft.

(b)
`A(w)=650w-2w^(2)`

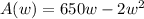
(c)Width = 162.5 feet

(d)
`52812.5 ft^(2)`

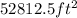
Explanation:

Let w be the width of the enclosure (perpendicular to the barn)

Let l be the length of the enclosure (parallel to the barn).

Perimeter of the fence = 650 feet

Since one side will be against the barn and we are fencing only three sides,

Perimeter = 2w+l

Therefore:

2w+l =650

• l=650-2w

Area of the pen A(l,w)=lw

Substituting l=650-2w into A(l,w)

`A(w)= w(650-2w)=650w-2w^(2)`

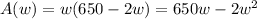
The dimension that will maximize the area of the pen occurs when the derivative of A(w)=0. (i.e. at the maximum point)

`A^(')(w)=650-4w`

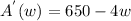
650-4w=0

4w=650

w=162.5 feet

Recall: l=650-2w

l=650 -2(162.5)=650-325=325 feet

l=325 feet

(a)The dimensions that will maximize the area of the pen is 162.5 ft by 325 ft.

(b)

If w =the width of the enclosure

l = the length of the enclosure.

Area of the enclosure = lw

`A(w)=650w-2w^(2)`

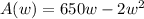
(c)Width, w that would maximize the area = 162.5 feet

(d)Maximum Area

`A(w)=650(162.5)-2(162.5)^(2)\\=105625-52812.5\\=52812.5 ft^2`