Answer:
(a) The sample variance for the daily price change is 0.2501.
(b) The sample standard deviation for the daily price change is 0.5001.
(c) The 95% confidence interval estimates of the population variance is (0.1255, 0.7210).
Explanation:
Let the random variable X denote the stock price changes for a sample of 12 companies on a day.
The data provided is:
X = {0.82 , 1.44 , -0.07 , 0.41 , 0.21 , 1.33 , 0.97 , 0.30 , 0.14 , 0.12 , 0.42 , 0.15}
(a)
The formula to compute the sample variance for the daily price change is:
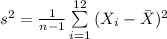
The sample mean is computed using the formula:
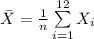
Consider the Excel output attached below.
In Excel the formula to compute the sample mean and sample variance are:
 =AVERAGE(A2:A13)
=AVERAGE(A2:A13)
 =VAR.S(A2:A13)
=VAR.S(A2:A13)
Thus, the sample variance for the daily price change is 0.2501.
(b)
The formula to compute the sample standard deviation for the daily price change is:
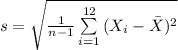
Consider the Excel output attached below.
In Excel the formula to compute the sample standard deviation is:
 =STDEV.S(A2:A13)
=STDEV.S(A2:A13)
Thus, the sample standard deviation for the daily price change is 0.5001.
(c)
The (1 - α)% confidence interval for population variance is:
![CI=[((n-1)s^(2))/(\chi^(2)_(\alpha/2) ) \leq \sigma^(2)\leq ((n-1)s^(2))/(\chi^(2)_(1-\alpha/2) ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/613t8kcs8mlrlbfbt21gwrf7ni0hquey04.png)
Compute the critical value of Chi-square for α = 0.05 and (n - 1) = (12 - 1) = 11 degrees of freedom as follows:
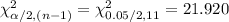
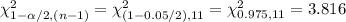
*Use a Chi-square table.
Compute the 95% confidence interval estimates of the population variance as follows:
![CI=[((n-1)s^(2))/(\chi^(2)_(\alpha/2) ) \leq \sigma^(2)\leq ((n-1)s^(2))/(\chi^(2)_(1-\alpha/2) ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/613t8kcs8mlrlbfbt21gwrf7ni0hquey04.png)
![=[((12-1)* 0.2501)/(21.920 ) \leq \sigma^(2)\leq ((12-1)* 0.2501)/(3.816) ]](https://img.qammunity.org/2021/formulas/mathematics/college/kdowbusn5vh1lgtlcs98i3vqj7nu4a0za5.png)
![=[0.125506\leq \sigma^(2)\leq 0.720938]\\\approx [0.1255, 0.7210]](https://img.qammunity.org/2021/formulas/mathematics/college/rszlrlcrspb99is5yr30es9pooycjo2ufw.png)
Thus, the 95% confidence interval estimates of the population variance is (0.1255, 0.7210).