Answer:
40.82% probability that 2 or more calls arrive in any 2 minute period.
Explanation:
We have the mean during a time interval, so we use the poisson distribution to solve this question.
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given time interval.
is the mean in the given time interval.
10 minutes.
3 outside calls, 4 inside. So mean of 3+4 = 7.
That is, 0.7 calls per minute.
Compute the probability that 2 or more calls arrive in any 2 minute period.
2 minutes, so
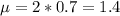
Either less than two calls arrive, or two or more do. The sum of the probabilities of these events is decimal 1. So
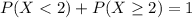
We want
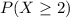 . So
. So
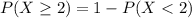
In which
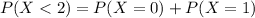



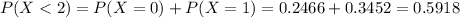
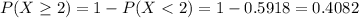
40.82% probability that 2 or more calls arrive in any 2 minute period.