Answer:
(a)
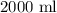 (b)
(b)
 (c)NO
(c)NO
Explanation:
GIVEN: Solution A is an
 acid solution. Solution B is a
acid solution. Solution B is a
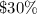 acid solution.
acid solution.
TO FIND: (a) Find the amount of Solution A (in mL) that must be added to
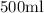 of Solution B in order to produce a
of Solution B in order to produce a
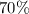 acid solution. (b) Find the amount of Solution A and Solution B (in mL) that can be combined in order to form a
acid solution. (b) Find the amount of Solution A and Solution B (in mL) that can be combined in order to form a
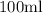 solution that is
solution that is
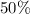 acid. (c) Does there exist a combination of Solution A and Solution B that is
acid. (c) Does there exist a combination of Solution A and Solution B that is
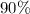 acid.
acid.
SOLUTION:
(a)
Let total amount of solution A added be

Total amount of mixture
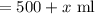
As resulting solution is
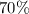 acid solution.
acid solution.
Amount of acid in final solution is sum of acid in both solutions
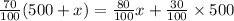
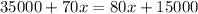
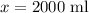
(b)
Let amount of Solution A be
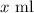
Amount of solution B

As resulting solution is
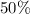 acidic solution
acidic solution
Amount of acid in final solution is sum of acid in both solutions
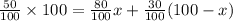
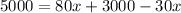
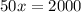
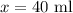
Amount of solution B
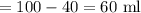
(c)
No as concentration of final solution can not be greater than one with higher concentration.