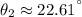Answer:
a)
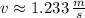 , b)
, b)
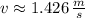 , c)
, c)
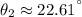
Step-by-step explanation:
a) The speed of the ball is determined by applying the Principle of Energy Conservation:
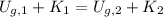
The speed of the ball when the string makes an angle of 12° with the vertical is:

![(1)/(2)\cdot m \cdot v^(2) = m\cdot g \cdot L \cdot [(1-\cos \theta_(1))-(1 -\cos \theta_(2))]](https://img.qammunity.org/2021/formulas/physics/high-school/uhd7egoagu8z4a5dptsok6w5tfvcnrn0c3.png)


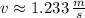
b) The maximum speed of the ball is:

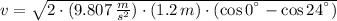
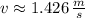
c) The angle between the string and the vertical when the speed of the ball is one-third its maximum value is obtained by proving different values of
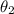 . The solution is approximately:
. The solution is approximately: