Question

Two identical objects (A, B) travel circles of the same radius, but object A completes three times as many rotations as object B in the same time.

The net centripetal force acting on object B is:

a) one-ninth the force acting on object A.
b) one-third the force acting on object A.
c) three times the force acting on object A.
d) nine times the force acting on object A.
e) the same as the force acting on object A.
Explain your choice.

Answer 1

a) One-ninth the force acting on object A.

Step-by-step explanation:

First, we derive an expression for the centripetal force acting on both objects.

For object A, centripetal force is:

`F_A = \frac{m{v_A}^2}{r}`

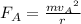
For object B, centripetal force is:

`F_B = \frac{m{v_B}^2}{r}`

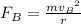
We are given that they have the same mass and they move in circles of the same radius.

If object A completes three times as many rotations as object B, then, object must have 3 times the speed of object B.

Hence:

`{v_A} = 3*{v_B}`

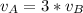
Therefore,
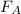`F_A` becomes:

`F_A = \frac{m({3*v_B}^(2) )}{r}\\\\\\F_A = \frac{9m{v_B}^(2)}{r}`

`F_A = 9F_B`

=>
`F_B = (1)/(9) F_A`

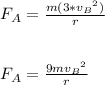
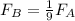
Therefore, the net centripetal force acting on object B is one-ninth of the force acting on object A.