Question

A number of reports in the medical literature suggest that the season of birth and the incidence of schizophrenia may be related, with a higher proportion of schizophrenics being born during the early months of the year. A study (78) following up on this hypothesis looked at 5139 persons born in England or Wales during the years 1921–1955 who were admitted to a psychiatric ward with a diagnosis of schizophrenia. Of these 5139, 1383 were born in the first quarter of the year. Based on census figures in the two countries, the expected number of persons, out of a random 5139, who would be born in the first quarter is 1292.1. Do an appropriate χ2 test with α = 0.05.

Answer 1

Explanation:

Hello!

The objective is to test id the variables

X₁: Season of birth of a person, Categorized in "first quarter of the year", "rest of the year"

X₂: Number of people with schizophrenia, admitted to a psychiatric ward.

To do so you need to conduct a hypothesis test using a Chi-Square for independence test.

The hypotheses for this test are:

H₀: Pij= Pi. * P.j

H₁: The random variables are not independent.

α: 0.05

`X^2= sum((O_(ij)-E_(ij)^2))/(E_(ij)) ~~X^2_((r-1)(c-1))`

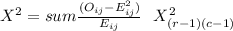
The first variable has two categories: "born in the first quarter of the year" and " born in the rest of the year"

And the second variable has only one category, "the patient has Schizophrenia"

You have then two expected values

One for the situation "the patient has schizophrenia and was born in the first quarter of the year" E₁₁= 2192.1

And the second for the situation "The patient has schizophrenia and wasn't born in the first quarter of the year" E₁₂= n - E₁₁ = 5139-1292.1= 3846.9

Note: For every Chi-Square test, be it Goodness to fit, Independence or Homogeneity test, the summary of all expected frequencies for all category combinations is always equal to the sample size.

The Observed frequencies between the years 1921 - 1955 are:

O₁₁= 1383

O₁₂= 3756

`X^2_(H_0)= ((1383-1292.1)^2)/(1292.1) + ((3756-3846.9)^2)/(3846.9)= 8.54`

Using the critical value approach, this test is always One-Tailed to the right:

`X^2_(1;0.95)= 3.841`

Decision rule

If
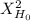`X^2_(H_0)` ≥ 3.841, the decision is to reject the null hypothesis.

If
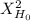`X^2_(H_0)` < 3.841, the decision is to not reject the null hypothesis.

The calculated Chi-Square value is greater than the critical value, the decision is to reject the null hypothesis.

Using a significance level of 5%, then you can conclude that the season a person was born and the incidence of schizophrenia are not independent, i.e. both variables are related.

I hope this helps!