Question

A(n) 71.1 kg astronaut becomes separated from the shuttle, while on a space walk. She finds herself 70.2 m away from the shuttle and moving with zero speed relative to the shuttle. She has a(n) 0.67 kg camera in her hand and decides to get back to the shuttle by throwing the camera at a speed of 12 m/s in the direction away from the shuttle. How long will it take for her to reach the shuttle? Answer in minutes. Answer in units of min.

Answer 1

10.347 minutes.

Step-by-step explanation:

According to F = ma, she exerts force on camera of the magnitude

F = 0.67Kg*12m/
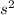`s^(2)` = 8.04N, assuming it took her one second to accelerate camera to 12m/s, then by newtons third law, which says every action has equal and opposite reaction , the camera exerts the same amount of force on the astronaut which gives her acceleration of a =
`(8.04N)/(70.2Kg) = 0.1130801680m/s^2`.

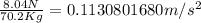and velocity of V = 0.1130801680m/s.

at this velocity , the astronaut has to cover the distance of 70.2 meters, it will take her 620.7985075s = 10.347 min to get to the shuttle (using S = vt).