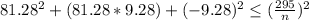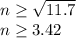Question

An AISI 1018 steel has a yield strength, Sy 5 295 MPa. Using the distortion-energy theory for the given state of plane stress,

(a) determine the factor of safety,
(b) plot the failure locus, the load line, and estimate the factor of safety by graphical measurement.

Answer 1

Complete Question:

An AISI 1018 steel has a yield strength,
`S_(y) = 295 MPa`. Using the distortion-energy theory for the given state of plane stress,

`\sigma_(x) = 31 MPa`,
`\sigma_(y) = 41 MPa` ,
`T_(xy) = 45 MPa`

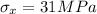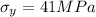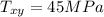
(a) determine the factor of safety,

(b) plot the failure locus, the load line, and estimate the factor of safety by graphical measurement.

Answer:

a) Factor of safety = 3.42

b) See the plot failure locus in the file attached

Step-by-step explanation:

According to the maximum distortion energy theorem:

`\sigma_(1) ^(2) - \sigma_(1) \sigma_(2) + \sigma_(2) ^(2) \leq ((S_(y) )/(n)) ^(2)`..............(1)

n = Factor of safety

We have to calculate
`\sigma_(1) and \sigma_(2)`

`\sigma_(1) = (\sigma_(x)+ \sigma_(y) )/(2) + \sqrt{((\sigma_(x)-\sigma_(y) )/(2)) ^(2) + T_(xy) ^(2) }`

`\sigma_(1) = (\sigma_(x)+ \sigma_(y) )/(2) - \sqrt{((\sigma_(x)-\sigma_(y) )/(2)) ^(2) + T_(xy) ^(2) }`

`\sigma_(1) = (31+ 41 )/(2) + \sqrt{((31-41 )/(2)) ^(2) +45 ^(2) }`

`\sigma_(1) = 81.28 MPa`

`\sigma_(2) = (31+ 41 )/(2) - \sqrt{((31-41 )/(2)) ^(2) +45 ^(2) }`

`\sigma_(2) = -9.28 MPa`

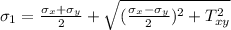
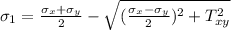
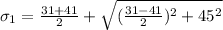
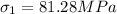
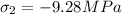
Substituting these values into equation (1)

`81.28 ^(2) +(81.28*9.28) + (-9.28) ^(2) \leq ((295 )/(n)) ^(2)`

`n^(2) \geq 11.7`

`n \geq √(11.7) \\n \geq 3.42`