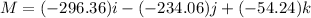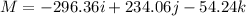Question

A gantry crane is dragging/lifting a crate from its current position using a single cable attached to the top center of the crate. If the tension in the cable, T, in kN, is 10 plus the last digit of your SID, Determine the force-moment system felt at O.

Answer 1

The force-moment system felt at O =

`F = -T = 8.28i + 7.52 j + 12.79 k`

`\\\\M = -296.36i +234.06j - 54.24k`

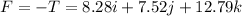
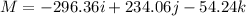
Step-by-step explanation:

The diagram shown below completes the other half of the question.As such, we will make sure to work in conjunction to that :

Given that;

the tension in the cable, T, in kN, is 10 plus the last digit of your SID,

T = (10 + 7)kN

T = 17 kN

Also; from the diagram ; Co-ordinates at points are

O (0,0,0)

A(6,12,9)

B(17,22,2)

However;

AB = OA - OB

AB = (6i + 12j + 19k) -(17i +22j + 2k)

AB = -11i -10j + 17 k

`|AB| = √((-11)^2+(-10^2)+(17)^2) \\\\|AB| = 22.58`

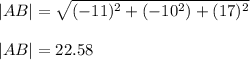
For the unit vector along AB is expressed as:

`\lambda_(AB) = (AB)/(22.58)\\\\\lambda = (-11i -10j+17k)/(22.58)`

Component of Tension
`T = \lambda_AB *T`

`T = (-11i-10j+17k)/(22.58)*17\\\\T = -8.28i -7.52j +12.79 k`

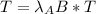
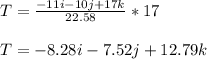
From the diagram , at point O; the reactive species generated are opposite in nature.

Therefore;
`F = -T = 8.28i + 7.52 j + 12.79 k`

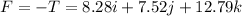
Also, to determine the moment of T about point O ; we have:

`\\\\M = AO * T = ( -6i - 12j - 19k ) * (-8.28i - 7.52j +12.79k)`

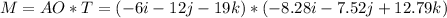
`\\M \left[\begin{array}{ccc}1&j&k\\-6&-12&-19\\-8.28&-7.52&12.79\end{array}\right]`

`\\\\\\M = [ (-12*12.79)-(-19*7.52)i - (-6)(12.79)-(-19)(-8.28)j+(-6)(-7.52)-(-12)(-8.28)]`

`\\\\M = (-296.36)i - (-234.06)j + (-54.24)k`

`\\\\M = -296.36i +234.06j - 54.24k`