Question

A survey of 100 MBA students found that 75 owned mutual funds, 35 owned stocks, and 15 owned both. a. What is the probability that a student owns a stock? What is the probability that a student owns a mutual fund? b. What is the probability that a student owns neither stocks nor mutual funds? c. What is the probability that a student owns either a stock or a mutual fund?

Answer 1

(a) The probability of the event that a student owns a stock is 0.35.

The probability of the event that a student owns a mutual fund.

(b)The probability that a student owns neither a stocks nor mutual is 0.5.

(c)The probability that a student owns either a stocks or a mutual fund is 0.80.

Explanation:

Probability:

Let the event space S of a given random experiment E be finite. If all the simple events connected to E be 'equally likely' then the probability of event A is defined as

`P(A)=\frac mn`

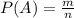
where n is total number of sample event and of these simple events are favorable.

Formula:

P(A∪B)=P(A)+P(B)-P(A∩B)

Given that,

A survey of 100 MBA students found that 75 owned mutual funds, 35 owned stocks and 15 owned both.

A = owned stocks

B= owned mutual funds

(a)

`P(A)=\frac{\textrm{Number of students who owned a stock}}{\textrm{Total nuber of students}}`

`=(35)/(100)`

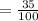
=0.35

`P(B)=\frac{\textrm{Number of students who owned a mutual funds}}{\textrm{Total nuber of students}}`

`=(75)/(100)`

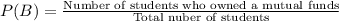
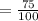
=0.75

The probability that a student owns a stocks=0.35.

The probability that a student owns a mutual funds=0.75.

The number of students who owned only a mutual fund

= Total number of students who owned a mutual fund - the number of students who owned both

=(75-15)

=60

The number of students who owned only a stock

= Total number of students who owned a stock- the number of students who owned both

=(35-15)

=20

The number students who owned either a stocks or a mutual fund or both is

= The number of students who owned only a mutual fund +The number of students who owned only a stock+the number of students who owned both

=60+20+15

=95

The number of students who owned neither a stocks nor mutual is

=100-95

=5

The probability that a student owns neither a stocks nor mutual is

=
`(5)/(100)`

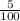
=0.05

(c)

The number of students who owned either a stocks or a mutual fund is

=60+20

=80

The probability that a student owns either a stocks or a mutual fund is

`=(80)/(100)`

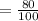
=0.80