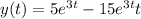Answer:
a) The general solution of the differential equation is
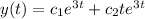 .
.
b) Applying the initial conditions the solution to the differential equation is then
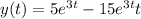 .
.
Explanation:
We have the following second order linear homogeneous differential equation with constant coefficients
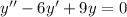
Given the differential equation
 ,
,
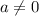 , consider the quadratic polynomial
, consider the quadratic polynomial
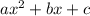 , called the characteristic polynomial. Using the quadratic formula, this polynomial always has one or two roots, call them
, called the characteristic polynomial. Using the quadratic formula, this polynomial always has one or two roots, call them
 and
and
 . The general solution of the differential equation is:
. The general solution of the differential equation is:
a)
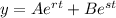 , if the roots
, if the roots
 and
and
 are real numbers and
are real numbers and
 .
.
b)
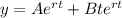 , if
, if
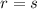 is real.
is real.
c)
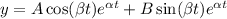 , if the roots
, if the roots
 and
and
 are complex numbers
are complex numbers
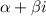 and
and
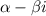 .
.
Applying the above information we have that:
The characteristic polynomial is
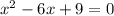
Its roots are
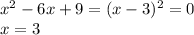
So, the general solution of the differential equation is:
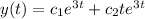
and its derivative is:
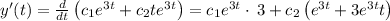
Now, plug in the initial conditions to get the following system of equations.
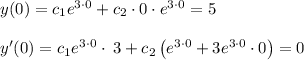
Solving this system gives
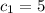 and
and
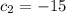
The actual solution to the differential equation is then