Question

We have 30 miles of fencing which can be used to enclose a rectangular piece of grazing land along a straight portion of a river. No fence is required along the river. The grazing land will be subdivided into two sections by means of a fence parallel to the sides and perpendicular to the river.

Write a function that expresses the total area in terms of the width x of the side of the grazing area perpendicular to the straight river.

Answer 1

The area of the gazing land is
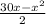`\frac{30x-x^2}2` square miles.

Explanation:

Given that, 30 miles of fencing can be used to enclose a rectangular piece of grazing land along a straight piece of river.

Let the length of the rectangular piece of gazing which is along the river be y and the width of the rectangular piece of gazing be x.

Along the river side, no fence is required.

Therefore total length of fence is = 2(x+y)-x

=2y+x

∴2y+x=30

⇒2y=30-x

`\Rightarrow y=(30-x)/(2)`

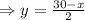
The area of the rectangular piece of gazing is = Length×width

=xy

`=x.\frac{30-x}2`

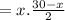
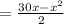`=\frac{30x-x^2}2` square miles.