Question

A Ferrari with a mass of 1400 kg approaches a freeway underpass that is 12 m across. Part A At what speed must the car be moving, in order for it to have a wavelength such that it might somehow "diffract" after passing through this "single slit"?

How do these conditions compare to normal freeway speeds of 30 ms?

Answer 1

To solve this problem, we will apply the concepts related to momentum both for an undulating particle given by the Planck constant and the wavelength, as well as the product between the mass and the speed. We will match the terms and then compare

`\text{Mass of the Ferrari} = m = 1400kg`

`\text{The Wavelength} = \lambda = 10m`

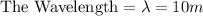
The momentum of the car is given as,

`P = (h)/(\lambda)`

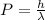
Here,

`h = \text{Plank's constant} = 6.63*10^(-34)J\cdot s`

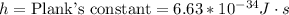
The momentum of the car related with the speed is

`P = mv`

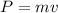
Equation we have

`mv = (h)/(\lambda)`

`v = (h)/(m\lambda)`

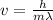
Replacing with our values we have that,

`v = ((6.63*10^(-34)J\cdot s))/((1400kg)(12m))`

`v = 3.946*10^(-38)m/s`

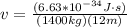
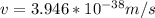
Now the wavelength will be

`\lambda = (h)/(mv)`

`\lambda = ((6.63*10^(-34)J\cdot s))/((1400kg)(30m/s))`

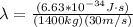
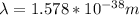`\lambda = 1.578*10^(-38)m` << 12 m

Therefore the speed is 30m/s, then we get the wavelength is less than 12m. The diffraction is not occurring