Question

A stone with a mass of 0.70 kg is attached to one end of a string 0.80 m long. The string will break if its tension exceeds 65.0 N. The stone is whirled in a horizontal circle on a frictionless tabletop; the other end of the string remains fixed. Find the maximum speed the stone can attain without breaking the string.

Answer 1

The maximum speed the stone can attain without breaking the string is 8.62 m/s .

Step-by-step explanation:

Given :

Mass of stone , m = 0.7 kg .

Length of string , l = 0.8 m .

It is also given that the stone will break if its tension exceeds 65.0 N.

Now , we know tension in the rope due to rotation is equal to the centripetal acceleration .

Therefore , the maximum speed the stone can attain without breaking the string is less than or equal to 65 N .

So ,
`(mv^2)/(r)=65`

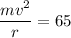
Putting all value in above equation we get :

`(0.7* v^2)/(0.8)=65\\\\v= 8.62\ m/s`

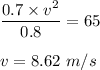
Therefore , maximum speed the stone can attain without breaking the string is 8.62 m/s .