Question

A coil is connected in series with a 12.6 kΩ resistor. An ideal 65.2 V battery is applied across the two devices, and the current reaches a value of 1.70 mA after 4.02 ms. (a) Find the inductance of the coil. (b) How much energy is stored in the coil at this same moment?

Answer 1

To solve the problem, start by applying the concepts related to current in an RL circuit. The current is defined exponentially and using Ohm's law we can put the initial current in terms of the voltage and resistance. Consecutively with the calculated time constant we can find the respective inductance. For the second part we will apply the electrical potential energy connectors to find the amount of stored energy.

PART A)

`i = i_0 (1-e^(-t/T))`

`i = (V/R)(1-e^(-t/T))`

`0.00402 = (65.2/12600)(1-e^(-0.00402/T))`

`T = 0.002679s`

`T = L/R`

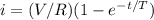
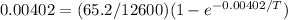
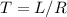
Inductance can be defined then,

`L = RT`

`L = (12600)(0.002679)`

`L = 33.75H`

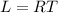
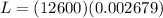
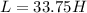
PART B) Now the energy is given under the terms:

`E = (1)/(2)Li^2`

`E = (1)/(2) (33.75)(0.00402)^2`

`E = 0.0002727J`

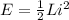
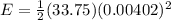
Therefore the energy stored in the coil at this same moment is 0.0002727J