Question

In a study of factors that affect whether students return to college after the first semester, one of the factors examined was the number of hours worked per week. The analysis revealed that students typically work an average of 18.1hours per week, with a standard deviation of 15.3 hours. If we consider a group of 700 freshmen at a community college, what is the probability that the average number of hours worked per week is more than 20 hours?

Answer 1

The probability that the average number of hours worked per week is more than 20 hours is 0.00052.

Explanation:

We are given that the analysis revealed that students typically work an average of 18.1 hours per week, with a standard deviation of 15.3 hours.

We consider a group of 700 freshmen at a community college.

Let
`\bar X` = sample average number of hours worked per week.

The z score probability distribution for sample average is given by;

Z =
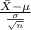`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = population average number of hours per week = 18.1 hours

`\sigma` = standard deviation = 15.3 hours

n = sample of freshmen = 700

Now, the probability that the average number of hours worked per week is more than 20 hours is given by = P(
`\bar X` > 20 hours)

P(
`\bar X` > 20 hours) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` >
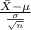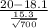`(20-18.1)/((15.3)/(√(700) ) )` ) = P(Z > 3.28) = 1 - P(Z
`\leq` 3.28)

= 1 - 0.99948 = 0.00052

The above probability is calculated by looking at the value of x = 3.28 in the z table which gives an area of 0.99948.

Therefore, the required probability is 0.00052.