Question

A cart with mass m vibrating at the end of a spring has an extra block added to it when its displacement is x=+A. What should the block's mass be in order to reduce the frequency to half its initial value? Express your answer in terms of the variables m and A.

Answer 1

The block's mass should be
`3m`

Step-by-step explanation:

Given:

Cart with mass
`m`

From the conservation of energy before mass is added,

`(1)/(2) mv^(2) = (1)/(2) kA^(2)`

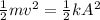
Where
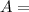`A =` amplitude of spring mass system,
`k =` spring constant

`A = v\sqrt{(m)/(k) }`

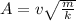
Now new mass
`M` is added to the system,

`(1)/(2) (m +M ) v^(2) = (1)/(2) k A^(2)`

`A = v \sqrt{(m +M )/(k) }`

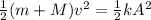
Here, given in question frequency is reduced to half so we can write,

`f' = (f)/(2)`

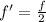
Where
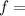`f =` frequency of system before mass is added,
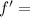`f' =` frequency of system after mass is added.

`\omega ' = (\omega)/(2)`

`\sqrt{(k)/(m +M) } = \frac{\sqrt{(k)/(m) } }{2}`

`(k)/(m +M ) = (k)/(4m)`

`M = 3m`

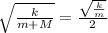
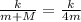
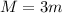
Therefore, the block's mass should be
`3m`