Question

A building window pane that is 1.44 m high and 0.96 m wide is separated from the ambient air by a storm window of the same height and width. The air space between the two windows is 0.06 m thick. If the building and storm windows are at 20 and −10°C, respectively, what is the rate of heat loss by free convection across the air space?

Answer 1

the rate of heat loss by convection across the air space = 82.53 W

Step-by-step explanation:

The film temperature

`T_f = (T_1+T_2)/(2) \\\\= (20-10)/(2)\\\\= (10)/(2)\\\\= 5^0\ C`

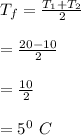
to kelvin = (5 + 273)K = 278 K

From the " thermophysical properties of gases at atmospheric pressure" table; At
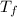`T_f` = 278 K ; by interpolation; we have the following

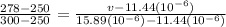`(278-250)/(300-250)= (v-11.44(10^(-6)))/(15.89(10^(-6))-11.44(10^(-6)))` → v 13.93 (10⁻⁶) m²/s

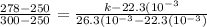`(278-250)/(300-250)= (k-22.3(10^(-3))/(26.3(10^(-3)-22.3(10^(-3)))` → k = 0.0245 W/m.K

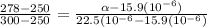`(278-250)/(300-250)= (\alpha - 15.9(10^(-6)))/(22.5(10^(-6)-15.9(10^(-6)))` → ∝ = 19.6(10⁻⁶)m²/s

`(278-250)/(300-250)= (Pr-0.720)/(0.707-0.720)` → Pr = 0.713

`\beta = (1)/(T_f) \\=(1)/(278) \\ \\ = 0.00360 \ K ^(-1)`

The Rayleigh number for vertical cavity

`Ra_L = (g \beta (T_1-T_2)L^3)/(\alpha v)`

=
`(9.81*0.00360(20-(-10))*0.06^3)/(19.6(10^(-6))*13.93(10^(-6)))`

=
`8.38*10^5`

`(H)/(L)= (1.44)/(0.06) \\ \\= 24`

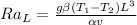
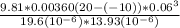
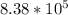
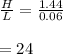
For the rectangular cavity enclosure , the Nusselt number empirical correlation:

`Nu_L = 0.42(8.38*10^5)^{(1)/(4)}(0.713)^(0.012)(24){-0.3}`

`NU_L= (hL)/(k)= 4.878`

`(hL)/(k)= 4.878`

`(h*0.06)/(0.0245)= 4.878`

`h = (4.878*0.0245)/(0.06)`

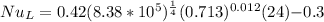
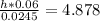
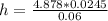
h = 1.99 W/m².K

Finally; the rate of heat loss by convection across the air space;

q = hA(T₁ - T₂)

q = 1.99(1.4*0.96)(20-(-10))

q = 82.53 W