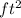Question

the boundary of a rectangular farm field in ireland has a straight rock wall along one side and fences along its other three sides. No fencing is necessary along the rock wall. Calculate the maximum area of field in square feet that can be enclosed using 2500 feet of fence

Answer 1

781250
`ft^(2)`

Explanation:

Let y is the length of the farm field

Let x is the width of the farm field

Given that, no fencing is necessary along the rock wall, so we can find the perimeter of the farm is:

2x + y = 2500 feet

<=> y = 2500 -2x

The are of the farm has the following formula:

A = x*y

<=> A = x(2500 - 2x)

<=> A = 2500x -2
`x^(2)`

To have the maximum area of field in square feet, we need to use differentials to estimate:

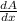`(dA)/(dx)` = 2500 - 4x

Set
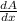`(dA)/(dx)` = 0, we have:

2500 - 4x = 0

<=> x = 625 feet.

=> y = 2500 - 2*625 = 1250 feet

So the maximum area of field is:

A = x*y = 625*1250 = 781250
`ft^(2)`