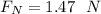Answer:
the speed of the car at the top of the vertical loop
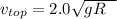
the magnitude of the normal force acting on the car at the top of the vertical loop
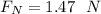
Step-by-step explanation:
Using the law of conservation of energy ;
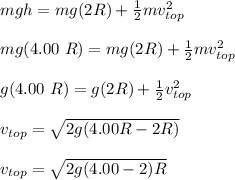
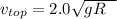
The magnitude of the normal force acting on the car at the top of the vertical loop can be calculated as:
![F_(N) = (mv^2_(top))/(R) \ - mg\\\\F_(N) = (m(2.0 √(gR))^2)/(R) \ - mg\\\\F_(N) = [(2.0^2-1]mg\\\\F_(N) = [(2.0)^2 -1) (50*10^(-3) \ kg)(9.8 \ m/s^2]\\\\](https://img.qammunity.org/2021/formulas/physics/college/3qbfkub0e5hwog8op8i5vutnz256dvapwj.png)