Question

A 4.00 kg mass is moving at 4.00 m/s 45.0 degrees NORTH of WEST and a 6.00 kg mass is moving at 3.00 m/s 30.0 degrees SOUTH of EAST. Find the velocity of the center of mass, letting (a) = the east-west component, and (b) = the north-south component.

Answer 1

Answer:

(a) 0.428 m/s

(b) 0.232 m/s

Step-by-step explanation:

mass, m = 4 kg

initial velocity, u = 4 m/s at 45° North of west = 4 ( - Cos 45 i + Sin 45 j)

`\overrightarrow{u}=- 2.83 \widehat{i} + 2.83 \widehat{j}`

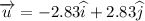
mass, M = 6 kg

initial velocity, U = 3 m/s at 30° South of east = 3 (Cos 30 i - Sin 30 j)

`\overrightarrow{U}=2.6 \widehat{i} -1.5 \widehat{j}`

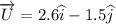
Let V is the velocity of centre of mass.

`\overrightarrow{V}=\frac{m* \overrightarrow{u}+M* \overrightarrow{U}}{m + M}`

`\overrightarrow{V}=\frac{4*\left ( - 2.83 \widehat{i} +2.83 \widehat{j} \right )+ 6* \left ( 2.6 \widehat{i} -1.5 \widehat{j} \right ) }{4 + 6}`

`\overrightarrow{V}= 0.428 \widehat{i}+0.232 \widehat{j}`

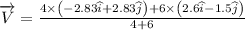
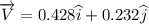
(a)

east west component of velocity of centre of mass is 0.428 m/s

(b)

north south component of velocity of centre of mass is 0.232 m/s.

Step-by-step explanation: