Question

A researcher is using a two-tailed hypothesis test with α = .05 to evaluate the effect of a treatment. If the boundaries for the critical region are t = ± 2.080, then how many individuals are in the sample?​

A. ​n = 22
B. ​n = 21
C. ​n = 20
D. ​Impossible to determine without more information

Answer 1

A. ​n = 22

Explanation:

Hello!

The researcher conducted a one-sample t-tas with the following hypotheses:

H₀: μ = μ₀

H₁: μ ≠ μ₀

α:0.05

The one-sample t-test has "n-1" degrees of freedom and since the hypotheses are two-tailed you know that the rejection region will be divided into two tails with "α/2" for each tail. ±
`t_(n-1;1-\alpha /2)`

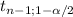
If α:0.05 then α/2:0.025 and 1-α/2= 0.975

Using the given sample sizes as a reference you look in the table for the corresponding DF for an accumulated probability of 0.975

For n = 22
`t_(21;0.975)= 2.080`

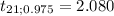
For n= 21
`t_(20;0.975)= 2.086`

For n= 20
`t_(19;0.975)= 2.093`

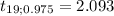
The correct answer is a) n= 22

I hope this helps!