Question

From a thin piece of cardboard 8 in. by 8 in., square corners are cut out so that the sides can be folded up to make a box. Determine the length of each side of the square corner to be cut that will produce the maximum volume of the box. Choose the answer that represents the sum of the dimensions (length + width + height) of the box of maximum volume.

Answer 1

The sum of dimensions is 12 in.

Explanation:

Given that, the dimension of the cardboard is 8 in by 8 in.

Let the length of side of the squares which are cut out from cardboard be x

The height of the folded box is = x in

The length of the folded box is =(8-2x) in.

The width of the folded box is = (8-2x) in.

Then the volume of the folded box is= Length × width × height

=(8-2x)(8-2x)x cubic in

=(64x-32x²+4x³) cubic in

Let,

V=64x-32x²+4x³

Differentiating with respect to x

V'= 64 -64x+12x²

Again differentiating with respect to x

V''= -64+24x

For maximum(or for the minimum value)

V'=0

⇒64 -64x+12x²=0

⇒4(3x²-16x+16)=0

⇒3x²-16x+16=0

⇒3x²-12x-4x+16=0

⇒3x(x-4)-4(x-4)=0

⇒(3x-4)(x-4)=0

`\Rightarrow x=\frac43, 4`

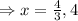
Now,
`V''|_(x=4)=-64+24* 4=32 >0`

`V''|_(x=\frac43)=-64+24* \frac43=-32 <0`

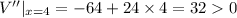
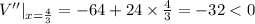
Since at
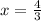`x=\frac43`, V''<0, So at
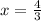`x=\frac43` , the volume of the box maximum

The height of the folded box is =
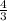`\frac43` in

The length of the folded box is
`=(8-2.\frac43)`

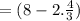
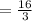`=\frac{16}3` in

The width of the folded box is
`=(8-2.\frac43)`

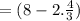
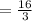`=\frac{16}3` in

The sum of dimensions is

=Length+width+height

`=(\frac{16}3+\frac{16}3+\frac43)` in

`=((16+16+4)/(3))` in

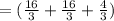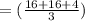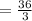`=\frac {36}3` in

=12 in