Question

(A) Construct a 95% confidence interval for the average width of an elevator rail. (B) How large a sample of elevator rails would we have to measure to ensure that we could estimate, with 95% confidence, the average diameter of an elevator rail within 0.01 inch

Answer 1

(a) The 95% confidence interval for the average width of an elevator rail is (2.048, 2.052).

(b) The sample size required is 4.

Explanation:

The width of 100 elevator rails have been measured. The sample mean and sample standard deviation of the elevator rails are 2.05 inches and 0.01 inches respectively.

According to the Central Limit Theorem if we have a population with mean μ and standard deviation σ and we take appropriately huge random samples (n ≥ 30) from the population with replacement, then the distribution of the sample mean will be approximately normally distributed.

Then, the mean of the distribution of sample means is given by,

`\mu_(\bar x)=\mu`

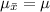
And the standard deviation of the distribution of sample means is given by,

`\sigma_(\bar x)=(\sigma)/(√(n))`

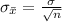
Since the sample size is quite large the population standard deviation can be estimated by the sample standard deviation.

So,
`\sigma_(\bar x)=(s)/(√(n))=(0.01)/(√(100))=0.001`

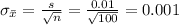
(A)

The (1 - α)% confidence interval for population mean (μ) is:

`CI=\bar x\pm z_(\alpha/2)* \sigma_(\bar x)`

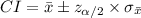
The critical value of z for 95% confidence level is:

`z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

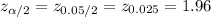
Compute the 95% confidence interval for the average width of an elevator rail as follows:

`CI=\bar x\pm z_(\alpha/2)* \sigma_(\bar x)`

`=2.05\pm 1.96* 0.001\\=2.05\pm 0.00196\\=(2.04804, 2.05196)\\\approx(2.048, 2.052)`

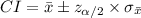
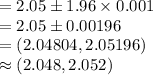
Thus, the 95% confidence interval for the average width of an elevator rail is (2.048, 2.052).

(B)

The margin of error of a (1 - α)% confidence interval for population mean (μ) is:

`MOE=z_(\alpha/2)* (s)/(√(n))`

Given:

MOE = 0.01

Compute the sample size as follows:

`MOE=z_(\alpha/2)* (s)/(√(n))`

`n=[(z_(\alpha/2)* s )/(MOE)]^(2)`

`=[(1.96* 0.01)/(0.01)]^(2)`

`=3.8416\\\approx 4`

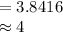
Thus, the sample size required is 4.