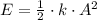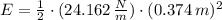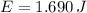Answer:
a)
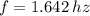 , b)
, b)
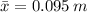 , c)
, c)
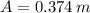 , d)
, d)
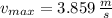 , e)
, e)
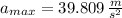 , f)
, f)
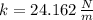 , g)
, g)
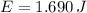
Step-by-step explanation:
a) The frequency is the reciprocal of the period of oscillation:
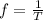
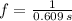
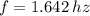
b) The equilibrium position is the average of the extreme points:
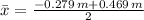
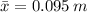
c) The amplitude is the absolute of the substraction of the equilibrium position from any of the extreme points:
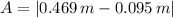
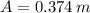
d) The angular frequency is:
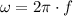
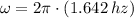
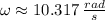
The maximum speed is:
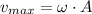
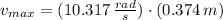
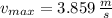
e) The maximum acceleration is:
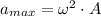
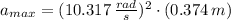
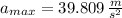
f) The force constant is:
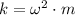
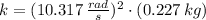
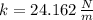
g) The total mechanical energy is: