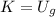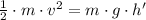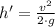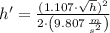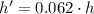Answer:
Step-by-step explanation:
The speed of the 0.5 kg block just before the collision is found by the Principle of Energy Conservation:
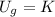
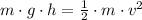
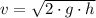
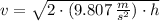

Knowing that collision is inelastic, the speed just after the collision is determined with the help of the Principle of Momentum Conservation:
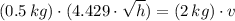
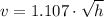
Lastly, the height reached by the two blocks is: