Question

A manufacturer of cordless electric shavers sampled 13 from a day's production and found the mean time of continuous usage without recharging to be 410 minutes with a sample standard deviation of 30 minutes. We can assume that times are normally distributed. We wish to test if the true mean operating time without recharging is more than 400 minutes.1. The correct calculated value of the test statistic is ____________.Options:A) -1.20B) 2.79C) -2.52D) -0.333E) 1.20

Answer 1

Option E) 1.20

Explanation:

We are given the following in the question:

Population mean, μ = 400 minutes

Sample mean,
`\bar{x}` = 410 minutes

Sample size, n = 13

Sample standard deviation, s = 30 minutes

Formula for test statistic:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

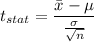
Putting all the values, we have

`t_(stat) = \displaystyle(410 - 400)/((30)/(√(13)) ) = 1.2018`

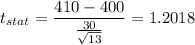
Thus, the value of test statistic is 1.20

The correct answer is

Option E) 1.20