Question

A coin slides over a frictionless plane and across an xy coordinate system from the origin to a point with xy coordinates (1.40 m, 7.20 m) while a constant force acts on it. The force has magnitude 4.50 N and is directed at a counterclockwise angle of 128.° from the positive direction of the x axis. How much work is done by the force on the coin during the displacement?

Answer 1

The work done required on the coin during the displacement is 21.75 w.

Step-by-step explanation:

Given that,

A coin slides over a friction-less plane i.e friction force = 0.

The co-ordinate of the given point is (1.40 m, 7.20 m).

The position vector of the given point is represented by
`1.40 \hat i+7.20 \hat j`.

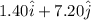The displacement of the coin is

`\vec d=1.40 \hat i+7.20 \hat j`

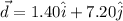
The force has magnitude 4.50 N and its makes an angle 128° with positive x axis.

Then x component of the force = 4.50 cos128°

The y component of the force = 4.50 sin128°

Then the position vector of the force is

`\vec F=(4.50 cos 128^\circ)\hat i+(4.50 sin 128^\circ)\hat j`

`=-2.77 \hat i+3.56 \hat j`

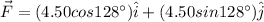
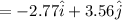
We know that,

work done is a scalar product of force and displacement.

`W=\vec F.\vec d`

`=(-2.77 \hat i+3.56 \hat j).(1.40 \hat i+7.20 \hat j)`

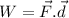
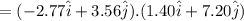
=(-2.77×1.40+ 3.56×7.20) w

=21.75 w

The work done required on the coin during the displacement is 21.75 w.