Question

During the dry month of August, one U.S. city has measurable rain on average only 4 days per month. Assume all months have 30 days. *(Round your answers to 1 decimal place.) **(Round the intermediate values to 4 decimal places. Round your answer to 4 decimal places.) (a) If the arrival of rainy days is Poisson distributed in this city during the month of August, what is the average number of days that will pass between measurable rain? *

Answer 1

The average number of days that will pass between measurable rain is 7.5.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given time interval.

The expected period between the event happening is
`(1)/(\mu)`

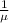
During the dry month of August, one U.S. city has measurable rain on average only 4 days per month. Assume all months have 30 days.

This means that

`\mu = (4)/(30)`

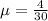
(a) If the arrival of rainy days is Poisson distributed in this city during the month of August, what is the average number of days that will pass between measurable rain? *

`(1)/((4)/(30)) = (30)/(4) = 7.5`

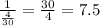
The average number of days that will pass between measurable rain is 7.5.