Question

A researcher compares the effectiveness of two different instructional methods for teaching anatomy. A sample of 293 students using Method 1 produces a testing average of 82.9. A sample of 282 students using Method 2 produces a testing average of 76.5. Assume that the population standard deviation for Method 1 is 7.97, while the population standard deviation for Method 2 is 6.66. Determine the 98% confidence interval for the true difference between testing averages for students using Method 1 and students using Method 2. Step 1 of 3 : Find the point estimate for the true difference between the population means.

Answer 1

The 98% confidence interval for the true difference between testing averages for students using Method 1 and students using Method 2 is (5.20, 7.60).

Explanation:

The (1 - α)% confidence interval for the difference between two population mean when the population standard deviations are known is:

`CI=(\bar x_(1)-\bar x_(2))\pm z_(\alpha/2)* \sqrt{(\sigma^(2)_(1))/(n_(1))+(\sigma^(2)_(2))/(n_(2))}`

The information provided is:

`\bar x_(1)=82.9\\\sigma_(1)=7.97\\n_(1)=293\\\bar x_(2)=76.5\\\sigma_(2)=6.66\\n_(2)=282`

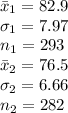
The critical value of z for 98% confidence interval is:

`z_(\alpha/2)=z_(0.02/2)=z_(0.0)=2.33`

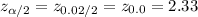
*Use a z-table for the critical value.

Compute the 98% confidence interval for the difference between two population means as follows:

`CI=(\bar x_(1)-\bar x_(2))\pm z_(\alpha/2)* \sqrt{(\sigma^(2)_(1))/(n_(1))+(\sigma^(2)_(2))/(n_(2))}`

`=(82.9-76.5)\pm 1.96* \sqrt{(7.97^(2))/(293)+(6.66^(2))/(282)}`

`=6.4\pm 1.199\\=(5.201, 7.599)\\\approx(5.20, 7.60)`

Thus, the 98% confidence interval for the true difference between testing averages for students using Method 1 and students using Method 2 is (5.20, 7.60).