Answer:
a)
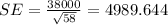
b) Normal and with the following parameters:
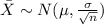
c)
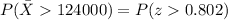
And using the complement rule and the normal standard distribution or excel we got:
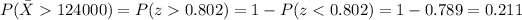
d)
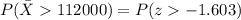
And using the complement rule and the normal standard distribution or excel we got:

Explanation:
Previous concepts
The central limit theorem states that "if we have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population with replacement, then the distribution of the sample means will be approximately normally distributed. This will hold true regardless of whether the source population is normal or skewed, provided the sample size is sufficiently large".
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
Solution to the problem
We know the following info:
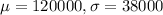
Part a
We select a sample of 58>30 households. From the central limit theorem we know that the distribution for the sample mean
 is given by:
is given by:
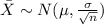
And the standard error is given by:
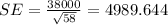
Part b
Normal and with the following parameters:
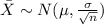
Part c
We can calculate the z score for 124000 and we got:
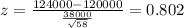
So we want this probability:
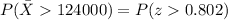
And using the complement rule and the normal standard distribution or excel we got:
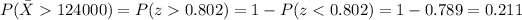
Part d
We can calculate the z score for 124000 and we got:
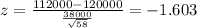
So we want this probability:
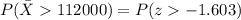
And using the complement rule and the normal standard distribution or excel we got:
