Question

What is the size of the payments that must be deposited at the beginning of each 6-month period in an account that pays 8.6%, compounded semiannually, so that the account will have a future value of $200,000 at the end of 10 years?

Answer 1

The answer is $86,167.57 (to 2 decimal places)

Step-by-step explanation:

In this question, we are to calculate the present value of a certain amount that is compounded semiannually, and after 10 years, yields a future value of $200,000. To calculate this, we will use the formula for calculating present value as follows:

PV = FV ÷
`(1+(r)/(n))^(n*t)`

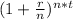
where:

PV = present value = ???

FV = future value = $200,000

r = interest rate in decimal = 8.6% = 0.086

n = compounding period pr year = semiannually = 2

t = time of compounding in years = 10

Therefore,

PV = 200,000 ÷
`(1+(0.086)/(2))^(2*10)`

PV = 200,000 ÷
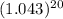`(1.043)^(20)` = $86,167.57