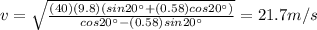Question

You’re driving your pickup car around a curve that has a radius of 40 m with a 20 degree bank to it. How fast can you drive around this curve with rubber tires on a concrete road without sliding off the road? (hint: look up the kinetic coefficient of friction)

Answer 1

21.7 m/s

Step-by-step explanation:

To solve this problem, we have to write the equations of motion along the two directions: horizontal and vertical.

Horizontal direction:

`N sin \theta + \mu N cos \theta = m(v^2)/(r)`

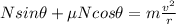
Vertical direction:

`N cos \theta - \mu N sin \theta - mg = 0`

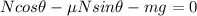
where:

N is the normal reaction on the car

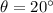`\theta=20^(\circ)` is the banking angle of the road

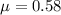`\mu=0.58` is the coefficient of friction of concrete

m is the mass of the car

v is the speed of the car

r = 40 m is the radius of the curve

`g=9.8 m/s^2`is the acceleration due to gravity

Combining the two equations together, we can find the maximum speed allowed for the car:

`v=\sqrt{(rg(sin \theta + \mu cos \theta))/(cos \theta - \mu sin \theta)}`

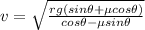
And substituting the data we have, we find:

`v=\sqrt{((40)(9.8)(sin 20^(\circ) + (0.58) cos 20^(\circ) ))/(cos 20^(\circ) - (0.58) sin 20^(\circ) )}=21.7 m/s`