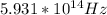Question

You've entered the Great Space Race. Your engines are hearty enough to keep you in second place. While racing, the person in front of you begins to have engine troubles and turns on his emergency lights that emit at a frequency of 5.880 x10¹⁴ Hz.

If the person in front of you is traveling 2626 km/s faster than you when he turns on his lights, what is the frequency of the emergency lights that you observe when it reaches you in your spaceship? (Enter your answer to four significant figures.)

Answer 1

To solve this problem we will apply the concepts related to the Doppler effect. The relationship given between the observed frequency and the actual frequency is given under the following mathematical function,

`(f_s)/(f_0) = \sqrt{(1+\beta)/(1-\beta)}`

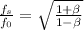
Here,

`\beta = (v)/(c) = (2626km/s)/(3*10^5km/s)`

`\beta = 0.008753`

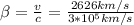
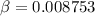
Rearrange the equation to obtain the frequency observed

`f_0 = f_s \sqrt{(1+\beta)/(1-\beta)}`

`f_0 = (5.88*10^(14))(\sqrt{(1+0.008753)/(1-0.008753)})`

`f_0 = 5.931*10^(14) Hz`

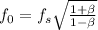
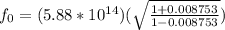
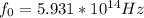
Therefore the frequency of the emergency lights that you observe when it reaches you in your spaceship is
`5.931*10^(14)Hz`