Answer:
The spurt of water takes 1 second to return to the jet's height.
Step-by-step explanation:
The height above the jet, h, of a spurt of water t seconds after leaving the jet can be given by the function as follows :
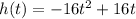 .......(1)
.......(1)
We need to find the time it takes for the spurt of water to return to the jet's height i.e. when h(t) = 0
Equation (1) becomes :
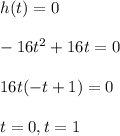
So, the spurt of water takes 1 second to return to the jet's height.