Question

A bank manager has developed a new system to reduce the time customers spend waiting for teller service during peak hours. The manager hopes the new system will reduce the waiting time that currently is 10 minutes. (a) Formulate the null and alternative hypotheses for this problem. (b) A random sample of 70 waiting times was obtained after the system was implemented. The sample showed a sample mean of 9.5 minutes and a standard deviation of 2.2 minutes. At what level of significance can you conclude that wait times have decreased?

Answer 1

(a) H₀: μ = 10 vs. Hₐ: μ < 10.

(b) The level of significance is 0.05.

Explanation:

A new system is used to reduce the time customers spend waiting for teller service during peak hours at a bank.

A single mean test can be used to determine whether the waiting time has reduced.

(a)

The hypothesis to test whether the new system is effective or not is:

H₀: The mean waiting time is 10 minutes, i.e. μ = 10.

Hₐ: The mean waiting time is less than 10 minutes, i.e. μ < 10.

(b)

The information provided is:

`\bar x=9.5\\s=2.2\\n=70`

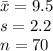
Compute the test statistic value as follows:

`t=(\bar x-\mu)/(s/√(n))=(9.5-10)/(2.2/√(70))=-1.902`

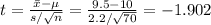
The test statistic value is t = -1.902.

Compute the p-value of the test as follows:

`p-value=P(t_(n-1)<t)`

`=P(t_(69)<-1.902)\\=P(t_(69)>1.902)\\=0.031`

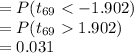
The null hypothesis will be rejected if the p-value of the test is less than the significance level (α).

The p-value obtained is 0.031.

To reject the null hypothesis the value of α should be more than 0.031.

The most commonly used values of α are: 0.01, 0.05 and 0.10.

So, the least value of α at which we can conclude that the wait times have decreased is, α = 0.05.

Thus, the level of significance is 0.05.