Question

. Suppose that n is a three-digit natural number, and 3 | n. If x is the 100s digit of n, y is the 10s digit of n, and z is the 1s digit of n, show that 3 | (x y z). (Hint: To understand the notation x, y, and z, suppose, for example, that n is the number 153. In this case, we get x

Answer 1

Proof is shown in the Explanation

Explanation:

Suppose that you have a three-digit number natural number n that is written xyz. Then

`n=10^2x+10y+z\\=(99+1)x+(9+1)y+z\\=(99x+9y)+(x+y+z)\\=3(33x+3y)+(x+y+z)`

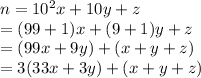
So when we divide n by 3, we obtain:

`(n)/(3) =(3(33x+3y)+(x+y+z))/(3) \\=33x+3y+(x+y+z)/(3)`

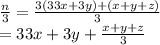
The remainder is clearly going to come from the division
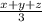`(x+y+z)/(3)`, since 33x+3y is an integer.

Since 3 divides n, the remainder is going to be a multiple of 3 and so we have shown that 3|(xyz).

Example:

Consider the number 336

`336=(100X3)+(10X3)+6\\=(99+1)3+(9+1)3+6=[99*3+9*3]+3+3+6\\=3(99+9)+12\\(336)/(3) =99+9 +(12)/(3) \\=99+9+4\\=112`