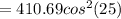Answer:
Without the third polarizer inserted in the middle of the first and second polarizer the irradiance of light that would emerge from the second polarizer is
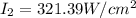
With the insertion of the third polarizer at the middle of the first and second polarizer the irradiance of light that would emerge from the second polarizer is

Step-by-step explanation:
From the question we are told that the
The angle between the transmission axis of first linear polarizer and the vertical axis is
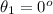
The angle between the transmission axis of second linear polarizer and the vertical axis is
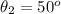
The angle between the transmission axis of third linear polarizer and the vertical axis is
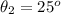
The irradiance of the incident natural light is
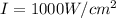
Generally a linear polarizer divides the irradiance of a natural light by 2
So For the first polarizer the irradiance of the natural light would become
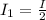
Substituting values
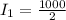
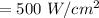
Now looking at the question we can deduce that the angle between the transmission axis of the and second polarizer is
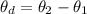
Substituting values
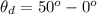
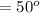
According to Malus Law the irradiance of light that would come out from the second polarizer is obtained by this mathematical expression
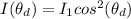
Substituting values
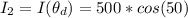
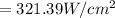
When the third polarizer is inserted between the first and second polarizer, we have that
The angle between the first polarizer and the third polarizer is mathematically evaluated as

Substituting the values
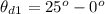
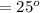
According to Malus Law the irradiance of light that would come out from the third polarizer is obtained by this mathematical expression
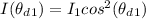
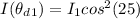
Substituting values
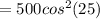
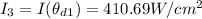
The angle between the third polarizer and the second polarizer is mathematically evaluated as
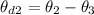
Substituting the values
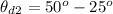 [Note the third polarizer is placed at the
[Note the third polarizer is placed at the
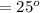 The middle of the first and second
The middle of the first and second
polarizer
According to Malus Law the irradiance of light that would come out from the second polarizer is obtained by this mathematical expression
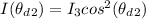
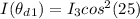
Substituting values