Question

A skater rotates with her arms crossed at an angular speed of 8.0 rad/s and she has a moment of inertia of 100 kg/m2. She extends her arms, and her angular speed drops to 7.0 rad/s. What is her moment of inertia now

Answer 1

When her hands extends, her momen of inertia is
`4.28\ kg-m^2`.

Step-by-step explanation:

Given that,

Initial angular speed,
`\omega_i=8\ rad/s`

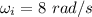
Initial moment of inertia,
`I_1=100\ kg-m^2`

Final angular speed,
`\omega_f=7\ rad/s`

Initially, a skater rotates with her arms crossed and finally she extends her arms. The momentum remains conserved. Using the conservation of momentum as :

`I_1\omega_1=I_2\omega_2`

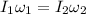
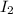`I_2` is final moment of inertia

`I_2=(I_1\omega_1)/(\omega_2)\\\\I_2=(100* 8)/(7)\\\\I_2=114.28\ kg-m^2`

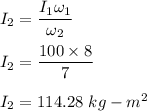
So, when her hands extends, her momen of inertia is
`4.28\ kg-m^2`. Hence, this is the required solution.