1 Answer

Thad · Answer 1 · 2021-12-23T05:34:25+0000

I suppose the equation should read

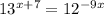
13^(x+7)=12^(-9x)

Take the logarithm of both sides; the base of the logarithm doesn't really matter, so I'll make the "natural" choice:

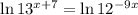
$\ln 13^(x+7)=\ln12^(-9x)$

Use the exponent property of logarithms:

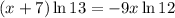
$(x+7)\ln13=-9x\ln12$

Solve for
:

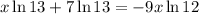
$x\ln13+7\ln13=-9x\ln12$

$x(\ln13+9\ln12)=-7\ln13$

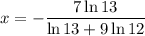
$x=-(7\ln13)/(\ln13+9\ln12)$

Then divide through the numerator and denominator by
$\ln13$ :

$x=-\frac7{1+9(\ln12)/(\ln13)}$

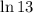Use the change of base formula to rewrite

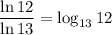
$(\ln12)/(\ln13)=\log_(13)12$

So we end up with one of many ways of expressing the solution:

$\boxed{x=-\frac7{1+9\log_(13)12}}$

Please log in or register to add a comment.