Answer:
(a) Correct option is (A).
(b) The value of P (X ≥ 770) is 0.0143.
(c) The value of P (X ≤ 720) is 0.0708.
Explanation:
Let X = number of elements with a particular characteristic.
The variable p is defined as the population proportion of elements with the particular characteristic.
The value of p is:
p = 0.74.
A sample of size, n = 1000 is selected from a population with this characteristic.
(a)
According to the Central limit theorem, if from an unknown population large samples of sizes n > 30, are selected and the sample proportion for each sample is computed then the sampling distribution of sample proportion follows a Normal distribution.
The mean of this sampling distribution of sample proportion is:
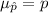
The standard deviation of this sampling distribution of sample proportion is:
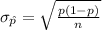
The sample selected is of size, n = 1000 > 30.
Thus, according to the central limit theorem the distribution of
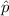 is Normal, i.e.
is Normal, i.e.
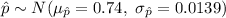 .
.
Thus the correct option is (A).
(b)
We need to compute the value of P (X ≥ 770).
Apply continuity correction:
P (X ≥ 770) = P (X > 770 + 0.50)
= P (X > 770.50)
Then
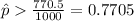
Compute the value of
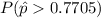 as follows:
as follows:
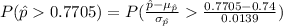
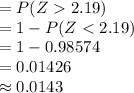
Thus, the value of P (X ≥ 770) is 0.0143.
(c)
We need to compute the value of P (X ≤ 720).
Apply continuity correction:
P (X ≤ 720) = P (X < 720 - 0.50)
= P (X < 719.50)
Then
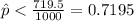
Compute the value of
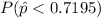 as follows:
as follows:
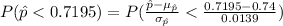
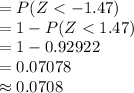
Thus, the value of P (X ≤ 720) is 0.0708.