Question

Clare made $160 babysitting last summer. She put the money in a savings account that pays 3% interest per year. If clare doesn't touch the money in her account, she can find the amount she'll have the next year by multiplying her current amount 1.03 a. Write an expression for the amount of money clare would have after 30 years if she never withdraws money from her account.

Answer 1

We have been given that Clare made $160 babysitting last summer. She put the money in a savings account that pays 3% interest per year. If Clare doesn't touch the money in her account, she can find the amount she'll have the next year by multiplying her current amount 1.03.

We are asked to write an expression for the amount of money Clare would have after 30 years if she never withdraws money from her account.

We will use exponential growth function to solve our given problem.

An exponential growth function is in form
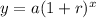`y=a(1+r)^x`, where

y = Final value,

a = Initial value,

r = Growth rate in decimal form,

x = Time.

`3\%=(3)/(100)=0.03`

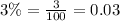
We can see that initial value is $160. Upon substituting our given values in above formula, we will get:

`y=160(1+0.03)^x`

`y=160(1.03)^x`

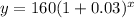
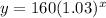
To find amount of money in Clare's account after 30 years, we need to substitute
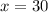`x=30` in our equation.

`y=160(1.03)^(30)`

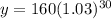
Therefore, the expression
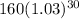`160(1.03)^(30)` represents the amount of money that Clare would have after 30 years.